Answer:
Because its graph will not pass the vertical line test.
Explanation:
We must first find the inverse of the given functions.
Let

.
Then for the first function, we have
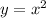
We interchange x and y to get,

We make y the subject to get,
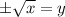
This is not a function because one x-value is mapping onto two y-values.
Hence its graph will not pass the vertical line test.
See red graph.
For the second function, we again let
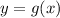
Then,
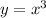
We interchange x and y to get,
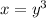
We make y the subject to get,
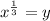
This is a function because, one x-value maps on to one and only one y-value. This tells us that the graph of this function will past the vertical line test.
see blue graph.