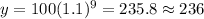Answer:
236 trucks will be registered in the city in Year 9.
Explanation:
The growth is given to be exponential. The general form of exponential function is,
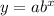
where a and b are constants.
The data given are
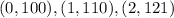
Putting
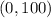 in the function,
in the function,
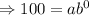
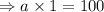
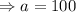
Putting the value in the function,
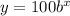
Putting
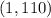 in the function,
in the function,
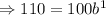
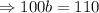
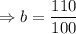
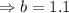
So the function becomes
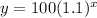
As we have to calculate the number of trucks registered in year 9, so putting x=9 in the function,