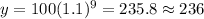Question

The table shows the number of trucks registered in a city each year. Suppose the growth continues exponentially.

How many trucks registered in the city in Year 9?
Round to the nearest whole number.
Enter your answer in the box.

Year 0 1 2
Number of trucks 100 110 121
_____
|____|

Answer 1

236

Explanation:

took the test and got it correct

Answer 2

236 trucks will be registered in the city in Year 9.

Explanation:

The growth is given to be exponential. The general form of exponential function is,

`y=ab^x`

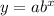
where a and b are constants.

The data given are
`(0,100),(1,110),(2,121)`

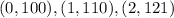
Putting
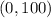`(0,100)` in the function,

`\Rightarrow 100=ab^0`

`\Rightarrow a* 1=100`

`\Rightarrow a=100`

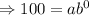
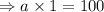
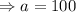
Putting the value in the function,

`y=100b^x`

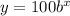
Putting
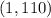`(1,110)` in the function,

`\Rightarrow 110=100b^1`

`\Rightarrow 100b=110`

`\Rightarrow b=(110)/(100)`

`\Rightarrow b=1.1`

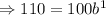
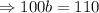
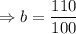
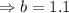
So the function becomes
`y=100(1.1)^x`

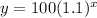
As we have to calculate the number of trucks registered in year 9, so putting x=9 in the function,

`y=100(1.1)^9=235.8\approx 236`