Question

Using Cramer's Rule, what are the values of x and y in the system of linear equations below??

Answer 1

A

Explanation:

simple

Answer 2

The value of x =-3 and y=1 in the system of linear equation.

Explanation:

Given equations

-2x+3y+z=7

-4x-y-2z=15

x+2y+3z=-7

Using cramer's rule to find x and y

First we make matrix of coefficient of x,y and z and then find the determinant

`A=\begin{bmatrix}-2&3&1\\-4&-1&-2\\1&2&3\end{bmatrix}`

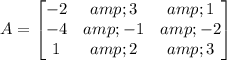
Now we find determinant of A

|A|=-2(-3+4)-3(-12+2)+1(-8+1)

|A|=21

`A_x=\begin{bmatrix}7&15&-7\\-4&-1&-2\\1&2&3\end{bmatrix}`

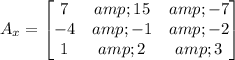
Determinant of Ax

|Ax|=7(-3+4)-3(45-14)+1(30-7)

|Ax|=-63

`A_y=\begin{bmatrix}7&15&-7\\-4&-1&-2\\1&2&3\end{bmatrix}`

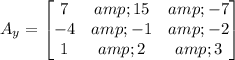
Determinant of Ay

|Ay|=-2(45-14)-7(-12+2)+1(28-15)

|Ay|=21

`A_z=\begin{bmatrix}-2&3&1\\-4&-1&-2\\7&15&-7\end{bmatrix}`

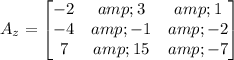
Determinant of Az

|Az|=-2(7-30)-3(28-15)+7(-8+1)

|Az|=-42

Now we find for x, y and z

`x=(|A_x|)/(|A|)\Rightarrow (-63)/(21)=-3`

`y=(|A_y|)/(|A|)\Rightarrow (21)/(21)=1`

`z=(|A_z|)/(|A|)\Rightarrow (-42)/(21)=-2`

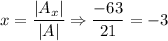
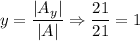
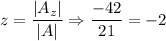
Thus, The value of x =-3 and y=1 in the system of linear equation.