Question

I really need help !

Answer 1

equation of sideway parabola is x = a( y - k )^2 + h or x = ax^2 + by + c

vertex : ( h,k ) = ( 1,2 )

x = a( y - 2 )^2 + 1 OR x = y^2 - 4y + 5

correct me if I am wrong

Answer 2

Answer: x =
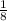`(1)/(8)`(y - 2)² + 1

Step-by-step explanation:

The vertex (h, k) is: (1, 2)

The formula for a sideways parabola is: x = a(y - k)² + h ; where a is the stretch and (h, k) is the vertex.

x = a(y - 2)² + 1

Now we need to find "a".

• Option 1: use the directrix to find the focus and calculate "a"
• Option 2: choose a point on the parabola, plug in that (x,y) value into the equation, and solve for "a".

Option 1:

directrix is -2 units from the vertex, so the focus (p) is +2 from the vertex.

`(1)/(4p)` = a

`(1)/(4(2))` = a

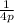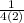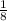`(1)/(8)` = a

Option 2:

I choose (9, -6) to replace (x, y)

x = a(y - 2)² + 1

9 = a(-6 - 2)² + 1

9 = a(-8)² + 1

8 = 64a

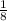`(1)/(8)` = a

Next, plug "a" into the equation: x =
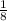`(1)/(8)`(y - 2)² + 1