Question

A pizza shop sells three sizes of pizza, and they track how often each size gets ordered along with how much they profit from each size. Let X represent the shop's profit on a randomly selected pizza. Here's the probability distribution of X along with summary statistics:

Small Medium Large
X = profit ($) 4 8 12
P(X) 0.18 0.50 0.32
Mean: μX = $8.56
Standard deviation: σx =$2.77
The company is going to run a promotion where customers get $2 off any size pizza. Assume that the promotion will not change the probability that corresponds to each size. Let Y represent their profit on a randomly selected pizza with this promotion. What are the mean and standard deviation of Y?

Answer 1

The mean and standard deviation of Y is $6.56 and $2.77 respectively.

Explanation:

Consider the provided information.

Let Y represent their profit on a randomly selected pizza with this promotion.

The company is going to run a promotion where customers get $2 off any size pizza.

Therefore,
`Y=\text{Profit}-\$2`

`Y=X-\$2`

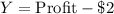
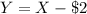
So the mean will be reduced by 2.

`\mu_Y=\mu_X-\$2`

`\mu_Y =\$ 8.56 - \$2`

`\mu_Y =\$6.56`

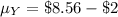
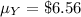
If we add or subtract any constant number from a given distribution, then the mean is changed by the same number(i.e constant number) but the standard deviation will remain the same.

Therefore
`\sigma_Y=\sigma_X=2.77`

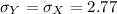
Hence, the mean and standard deviation of Y is $6.56 and $2.77 respectively.