Question

Write an exponential equation for each coin that will give the coins value,v,at any time,t use the formula? Coin A worth $25 and increase by 7% each year and coin B worth $40

increase by 5% each year

Answer 1

1) for the coin A its value to first year , is

a1 = 25+25(7/100)= 25[1+7/100]

the second year a2 = a1 + 7/100 a1

a2 = 25+25(7/100) + [25+25(7/100)]7/100

a2= 25+25(7/100) + 25(7/100) + 25(7/100)^2

a2=25[1+7/100]^2

in t years will be at = 25[1+7/100]^t =25[1+0,07]^t

for the coin B IS THE SAME PROCEDURE

bt = 40[1+0,05]^t

Answer 2

Answer: For coin A,

`v=25(1.07)^t`

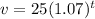
For coin B,

`v=40(1.05)^t`

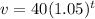
Explanation:

The exponential equation is,

`y=ab^x`

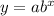
Where, a is the initial value,

b is the growth or decay factor,

Since, Coin A worth $25 and increase by 7% each year,

So, the coin A's value after t years,

`v=25(1+(7)/(100))^t`

`v=25(1+0.07)^t`

`\implies v=25(1.07)^t`

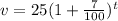
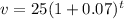
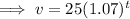
Which is the required equation for coin A.

Now, Coin B worth $40 increase by 5% each year,

So, the coin B's value after t years,

`v=40(1+(5)/(100))^t`

`v=40(1+0.05)^t`

`\implies v=40(1.05)^t`

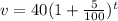
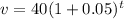
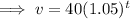
Which is the required equation for coin B.