Question

A solid sphere of brass (bulk modulus of 14.0 3 1010 n/m2) with a diameter of 3.00 m is thrown into the ocean. by how much does the diameter of the sphere decrease as it sinks to a depth of 1.00 km?

Answer 1

The diameter of the sphere decrease is 0.124 m.

Step-by-step explanation:

Given that,

Bulk modulus
`B= 14.03*10^(10)\ N/m^2`

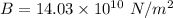
Diameter d = 3 m

Depth = 1.00 km

Pressure
`\Delta P=\rho gh=1000*9.81*1*10^3`

`\Delta P= 9.81*10^(6)\ N/m^2`

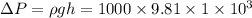
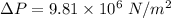
Volume
`V =(4)/(3)\pi r^3`

`(\Delta V)/(V)=((\Delta r)^3)/(r^3)`

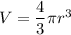
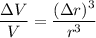
Formula of the bulk modulus is define as,

`B =- (\Delta P)/((\Delta V)/(V))`

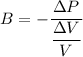
Where,
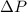`\Delta P` = Change in pressure

V = volume

Put the value into the formula

`B=-(9.81*10^(6)*(r)^3)/((\Delta r)^3)`

`(\Delta r)^3=-(9.81* 10^6*(1.5)^3)/(14.03*10^(10))`

`(\Delta r)^3=-(9.81* 10^6*(1.5)^3)/(14.03*10^(10))`

`(\Delta r)=-((9.81* 10^6*(1.5)^3)/(14.03*10^(10)))^{(1)/(3)}`

`\Delta r=-0.062\ m`

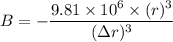
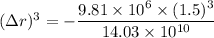
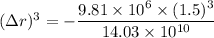
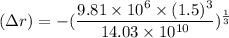
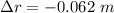
Change in diameter

`\Delta d=-2*0.062\ m`

`\Delta d=-0.124\ m`

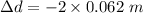
Hence, The diameter of the sphere decrease is 0.124 m.

Answer 2

As per the formula of bulk modulus we know that

`B = (\Delta P)/(\Delta V/V)`

as we know that

`V = (4)/(3)\pi R^3`

`\Delta V = 4 \pi R^2 \Delta R`

now we will have

`\Delta V/ V = (3\Delta R)/(R)`

now we will have from above equation

`\Delta V/ V = (\Delta P)/(B)`

`(3\Delta R)/(R) = (\rho g h)/(B)`

`(3 \Delta R )/(3) = (10^3 * 9.8 * 1000)/(14 * 10^(10))`

`\Delta R = 7 * 10^(-5) m`