Answer:
The diameter of the sphere decrease is 0.124 m.
Step-by-step explanation:
Given that,
Bulk modulus
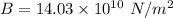
Diameter d = 3 m
Depth = 1.00 km
Pressure
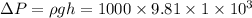
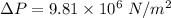
Volume
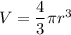
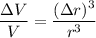
Formula of the bulk modulus is define as,
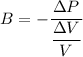
Where,
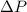 = Change in pressure
= Change in pressure
V = volume
Put the value into the formula
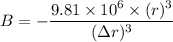
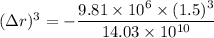
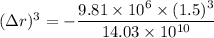
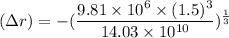
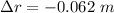
Change in diameter
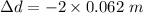
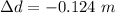
Hence, The diameter of the sphere decrease is 0.124 m.