Answer: The following three equations could be used to determine the rate:
x*(time there) = 3 miles
(x+1)*(time back) = 3 miles
(time there) + (time back) = 2.5 hr
Step by step (including the actual solution x):
Equation for the trip there:
x*(time there) = 3 miles
Equation for the trip back:
(x+1)*(time back) = 3 miles
And we also know that:
(time there) + (time back) = 2.5 hr
So we have three equations with three unknowns and can solve for x. Let us call
(time there): t1
(time back): t2
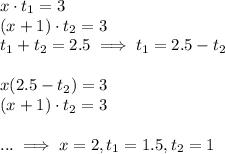
The solution (I skipped the gory details of solving, but you can verify by plugging the values back into the equations) is
Rate x = 2 miles/hour
(time there) = 1.5 hours
(time back) = 1 hour