A science teacher needs to choose 12 out of 16 students to serve as peer tutors how many different ways can the teacher choose the 12 students

Question

asked Dec 20, 2019 172k views

2 Answers

Boba Fett Likes JS · Answer 1 · 2019-12-24T12:55:58+0000

Answer:

1820 ways.

Explanation:

We have been given that a science teacher needs to choose 12 out of 16 students to serve as peer tutors.

We will use combinations to solve our given problem.

The formula
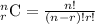$_(r)^(n)\textrm{C}=(n!)/((n-r)!r!)$ represents number of ways to choose r items from n total items.

Upon substituting our given values in above formula, we will get:

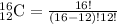
$_(12)^(16)\textrm{C}=(16!)/((16-12)!12!)$

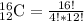
$_(12)^(16)\textrm{C}=(16!)/(4!*12!)$

$_(12)^(16)\textrm{C}=(16*15*14*13*12!)/(4*3*2*1*12!)$

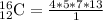
$_(12)^(16)\textrm{C}=(4*5*7*13)/(1)$

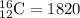
$_(12)^(16)\textrm{C}=1820$

Therefore, the tutors can be chosen in 1820 different ways.