Let the cup is filled to height h after some time
now the total volume of coffee filled in the cup is given as
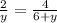
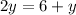
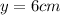
now volume of the coffee will be
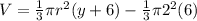
here we know that
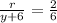
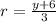
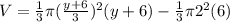
now we know that volume flow rate is given as

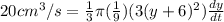
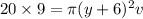
here y = 3 cm
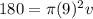

so water will rise up with speed 0.71 cm/s