Answer:
Length of arc BC is 14 centimeter.
Explanation:
Point A, B and C lie on a circle with center Q.
The area of sector AQB is twice the area of sector BQC.
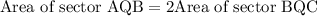
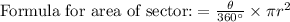
Let sector AQB subtended angle
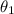 at centre.
at centre.
Let sector BQC subtended angle
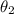 at centre.
at centre.
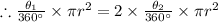
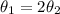
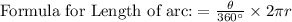
Length of arc AB is 28 centimeters.
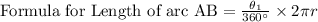

Length of arc BC is l centimeters.
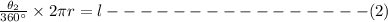
Divide equation 1 by equation 2 and we get
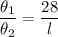
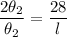
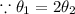
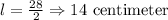
Thus, Length of arc BC is 14 centimeter.