Question

Points A, B and C lie on a circle with center Q.

~ The area of sector AQB is twice the area of sector BQC.

~ The length of arc AB is 28 centimeters.

What is the length, in centimeters, of arc BC?

Answer 1

Length of arc BC is 14 centimeter.

Explanation:

Point A, B and C lie on a circle with center Q.

The area of sector AQB is twice the area of sector BQC.

`\text{Area of sector AQB}=2\text{Area of sector BQC}`

`\text{Formula for area of sector:} =(\theta)/(360^(\circ))* \pi r^2`

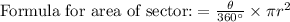
Let sector AQB subtended angle
`\theta_1` at centre.

Let sector BQC subtended angle
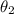`\theta_2` at centre.

`\therefore (\theta_1)/(360^(\circ))* \pi r^2=2* (\theta_2)/(360^(\circ))* \pi r^2`

`\theta_1=2\theta_2`

`\text{Formula for Length of arc:} =(\theta)/(360^(\circ))* 2\pi r`

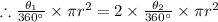
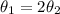
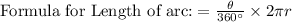
Length of arc AB is 28 centimeters.

`\text{Formula for Length of arc AB} =(\theta_1)/(360^(\circ))* 2\pi r`

`(\theta_1)/(360^(\circ))* 2\pi r=28--------------(1)`

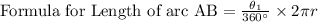
Length of arc BC is l centimeters.

`(\theta_2)/(360^(\circ))* 2\pi r=l----------------(2)`

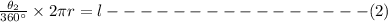
Divide equation 1 by equation 2 and we get

`(\theta_1)/(\theta_2)=(28)/(l)`

`(2\theta_2)/(\theta_2)=(28)/(l)`
`\because \theta_1=2\theta_2`

`l=(28)/(2)\Rightarrow 14\text{ centimeter}`

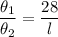
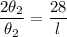
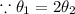
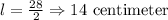
Thus, Length of arc BC is 14 centimeter.