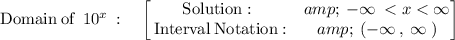Answer:
The domain is all real number:
i.e.
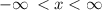
Therefore,
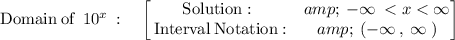
Explanation:
Given the function
y = 10ˣ
Determining the domain of the function y = 10ˣ :
We know that the domain of the function is the set of input or arguments for which the function is real and defined.
In other words,
- Domain refers to all the possible sets of input values on the x-axis.
From the graph, it is clear that the function has no undefine points nor domain constraints.
Thus, the domain is all real number:
i.e.
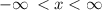
Therefore,