Answer: Choice (D): x<=-2 or x>=8
Step-by-step explanation:
An absolute value |x| is a function that has a "tricky" definition: it equals x is x >=0, but changes abruptly to -x for values of x<0.
This two-case scenario has to be respected and built into a solution of any equation or inequality involving absolute values.
So we start treating the inequality for two cases:
(1) for the case when x-3 >=0, fo which the absolute value is the same what is inside the vertical brackets:

(2) for the other case of x-3<0, in which case we need that extra minus sign:
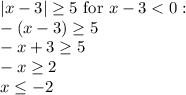
So putting both cases together, the solution to the inqueality is an x falling to either of the two intervals: x>=8 or x<=-2, which corresponds to choice (D).