Question

Algebra is not epic or I just don't know how to do it, and in a state of angered ignorance I have come here to seek help

Answer 1

Answer: Choice (D): x<=-2 or x>=8

Step-by-step explanation:

An absolute value |x| is a function that has a "tricky" definition: it equals x is x >=0, but changes abruptly to -x for values of x<0.

This two-case scenario has to be respected and built into a solution of any equation or inequality involving absolute values.

So we start treating the inequality for two cases:

(1) for the case when x-3 >=0, fo which the absolute value is the same what is inside the vertical brackets:

`|x-3|\geq5\,\,\mbox{for}\,\, x-3\geq0:\\x-3 \geq 5\\x\geq 8\\`

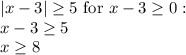
(2) for the other case of x-3<0, in which case we need that extra minus sign:

`|x-3|\geq5\,\,\mbox{for}\,\, x-3<0:\\-(x-3)\geq 5\\-x + 3\geq 5\\-x \geq 2\\x \leq -2`

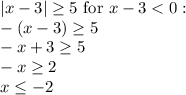
So putting both cases together, the solution to the inqueality is an x falling to either of the two intervals: x>=8 or x<=-2, which corresponds to choice (D).