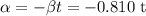Answer : The angular acceleration is
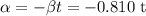
Solution : Given,
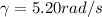
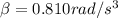
The given angular velocity equation is,

At t = 0,
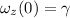
At t = t,

Formula used for angular acceleration :
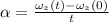
where,
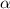 = angular acceleration
= angular acceleration
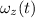 = angular velocity at time 't'
= angular velocity at time 't'
 = angular velocity at time '0'
= angular velocity at time '0'
t = time
Now put all the given values in this formula, we get the angular acceleration.

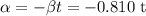
Therefore, the angular acceleration is