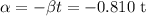Question

A fan blade rotates with angular velocity given by ωz(t)= γ − β t2, where γ = 5.20 rad/s and β = 0.810 rad/s3 . calculate the angular acceleration as a function of time t in terms of β and γ.

Answer 1

Answer : The angular acceleration is
`\alpha=-\beta t=-0.810\text{ t}`

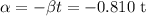
Solution : Given,

`\gamma=5.20rad/s`

`\beta=0.810rad/s^3`

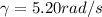
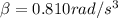
The given angular velocity equation is,

`\omega_z(t)=\gamma-\beta t^2`

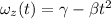
At t = 0,
`\omega_z(0)=\gamma`

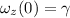
At t = t,
`\omega_z(t)=\gamma-\beta t^2`

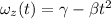
Formula used for angular acceleration :

`\alpha=(\omega_z(t)-\omega_z(0))/(t)`

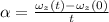
where,

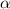`\alpha` = angular acceleration

`\omega_z(t)` = angular velocity at time 't'

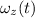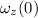`\omega_z(0)` = angular velocity at time '0'

t = time

Now put all the given values in this formula, we get the angular acceleration.

`\alpha=((\gamma)-(\gamma-\beta t^2))/(t)`

`\alpha=-\beta t=-0.810\text{ t}`

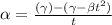
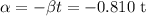
Therefore, the angular acceleration is
`\alpha=-\beta t=-0.810\text{ t}`