Answer: The proof is mentioned below.
Explanation:
Let a/b and c/d are two rational numbers where b ≠ 0 and d ≠ 0 ( by the property of rational number.) And, a, b, c and d are integers.
Proof that:
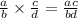 is also a rational number, for which bd≠ 0
is also a rational number, for which bd≠ 0
Since a and b are integers therefore ab are also integers ( because integers are closed under multiplication)
Similarly cd is also an integer.
⇒
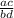 is a fraction in which both numerator and denominator are integers.
is a fraction in which both numerator and denominator are integers.
Moreover, b≠0 and d≠0 ⇒ bd≠0 ( because product of non zeros number is also non zero.)
Thus, by the property of rational number
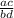 is also a rational number for which bd≠ 0
is also a rational number for which bd≠ 0
Therefore, The product of two rational is numbers always rational.