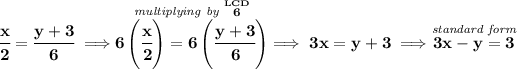let's bear in mind that
standard form for a linear equation means
• all coefficients must be integers, no fractions
• only the constant on the right-hand-side
• all variables on the left-hand-side, sorted
• "x" must not have a negative coefficient
so, let's do away with the denominators by multiplying both sides by the LCD of all fractions, in this case 6.