Question

Write the equation of the ellipse with center at (21), one vertex at (2-4), and one focus at (2,-2)

Answer 1

B. (x-2)^2/16 + (y-1)^2/25=1

Answer 2

`((x-2)^2)/(16) +((y-1)^2)/(25) =1`

Explanation:

The equation of an ellipse outside the origin is as follows

`((x-h)^2)/(a^2) +((y-k)^2)/(b^2) =1`

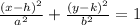
The above is for an ellipse centered on (h, k). in this case the center is in (2,1) so
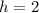`h = 2` and
`k = 1`

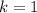
So far we have:

`((x-2)^2)/(a^2) +((y-1)^2)/(b^2) =1`

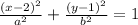
Now we find a and b, Where b is the semi-major axis and the minor semi-axis.

If the center is at (2, 1) and one focus is at (2,-2) this means there are 3 units of distance between the center and the focus. This quantity will be called c.

`c=3`

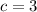
Now, of one vertex is at (2,-4) this means there are 5 units of distance between the center and the vertex, this is the semi major axis of the ellipse

`b= 5` ⇒
`b^2=5^2=25`

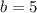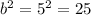
and to find a:

`b^2=a^2+c^2`

clearing for a:

`a^2=b^2-c^2`

`a^2=5^2-3^2`

`a^2=25-9`

`a^2=16`

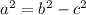
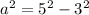
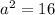
Substituting in the equation of the ellipse

`((x-2)^2)/(16) +((y-1)^2)/(25) =1`

wich is the second of the options.