Question

1.) While setting up a fireworks display, you have a tool at the top of the building and need to drop it to a coworker below.

a.) how long will it take the tool to fall to the ground? (hint: use the first equation that you were given above, h(t) = -16t^2 + h0 ) For the building's height, use the height of the building you estimated in task one (70ft tall)

b.) Draw a graph that represents the path of this tool falling tonthe ground. Your graph should show the height of the tool after t seconds have passed. Label this line "tool"

PLEASE SHOW YOUR WORK!

Answer 1

It's important to notice that the person is on the top of the building, so its position is the same as the height of the building.

Additionally, the movement is defined by

`h(t)=-16t^(2)+h_(0)`

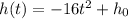
Where
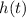`h(t)` is the height at any moment, and
`h_(0)` is the initial height (the same as the building's).

So, we know the building is 70 feet tall, that means
`h_(0) =70`.

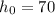When the tool hits the ground its height is zero, so
`h(t)=0`.

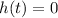Replacing these values, we have

`h(t)=-16t^(2)+h_(0)\\0=-16t^(2)+70`

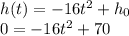
Solving for
`t`

`16t^(2)=70\\ t^(2)=(70)/(16)=4.375\\ t=√(4.375)\\ t \approx 2.09`

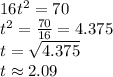
So, it took 2.09 seconds to hit the ground.

On the other hand, to dra a graph that represents the movement of the tool, we just need to graph the quadratic function we used.

The image attached shows the graph of this situation.

Also, the falling red curve shows the height at any second.

Answer 2

`h(t)=-16t^2+70`

The time to reach ground is 2.09165 sec

Explanation:

(a)

we are given

`h(t)=-16t^2+h_0`

we are given

height of the building is 70ft

so, at t=0 , h(t)=70

so, we can use it

`h(0)=-16(0)^2+h_0`

`70=-16(0)^2+h_0`

`h_0=70`

now, we can plug it back

`h(t)=-16t^2+70`

On ground , height becomes 0

so, we can set h(t)=0

and then we can solve for t

`h(t)=-16t^2+70=0`

`t^2=(35)/(8)`

`t=(√(70))/(4),\:t=-(√(70))/(4)`

Since, we can only consider positive value

and we get

`t=2.09165`

(b)

we can draw graph