Answer:
It's important to notice that the person is on the top of the building, so its position is the same as the height of the building.
Additionally, the movement is defined by
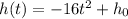
Where
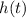 is the height at any moment, and
is the height at any moment, and
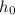 is the initial height (the same as the building's).
is the initial height (the same as the building's).
So, we know the building is 70 feet tall, that means
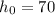 .
.
When the tool hits the ground its height is zero, so
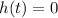 .
.
Replacing these values, we have
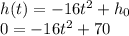
Solving for
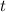
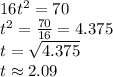
So, it took 2.09 seconds to hit the ground.
On the other hand, to dra a graph that represents the movement of the tool, we just need to graph the quadratic function we used.
The image attached shows the graph of this situation.
Also, the falling red curve shows the height at any second.