1. It is given that f(x) is 16 times the square root of x.
Putting that in mathematical terms we have,
f(x) = 16 *
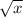
also, y = f(x)
So, we have the function
y= 16
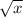
4. We need to solve the inequality equation : 4x + 2y ≤ 6
Let us take the equation,
4x+2y ≤ 6
2y ≤ 6-4x
y ≤
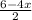
y ≤ 3-2x
So, any point (x,y) lies on the given inequality region, where y≤ 3-2x
5. Solving system of equations using addition method
Given:
-5x-y =38 ------> a
-6x-3y =60 -------> b
Divide the equation b by no. 3
(-6x-3y)/3 = 60/3
-2x-y = 20 -------> c
Subtracting equation c from a we have,
-5x-y - (-2x-y) = 38 - 20
-5x-y+2x+y = 18
-3x = 18
x = -6
Now, substituting the value of x in equation a, we get
-5(-6) - y =38
30-y =38
y= 30-38 = -8
y=-8
∴ x = -6 and y = -8
6. Finding composition of functions
Given : f(x) =15x + 7 ; g(x) = x² - 5x
To find : (f+g)(x)
(f+g) (x) = f(g(x))
So, replace the value of x in f(x) by g(x), where g(x)= x² - 5x
(f+g)(x) = 15(x²-5x) +7 =15x²-75x+7
∴ (f + g)(x) = 15x²-75x+7
7. System of 3 equations must be solved to find the solution
-8x-8y-5z=-6
7x-8y-9z =17
9x+2y+6z =-1
Solving by substitution method.
Isolate x from first equation :
x= (-6+8y+5z)/(-8)
Substitute this value of x in 2nd and 3rd equations.
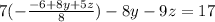
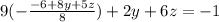
Now, isolating y from the 2nd equation rewritten above, we have
y= -
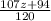
Now substituting this value of y in the 3rd equation rewritten above, we have

Isolating z from above equation, we have
z = -2
Substitute z= -2 in the equation of y, we have
y= -
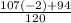 = 1
= 1
y = 1
Substituting the value of y and z, in the equation of x, we have
x= (-6+8(1)+5(-2))/(-8) = 1
x = 1
∴ x=1 ; y = 1 ; z = -2
8. 5x ≤ 7
Solving the above equation, we have
x ≤ 7/5
Please see attachment for the graph.
9. The given function is : g(y) =
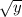 -6
-6
The domain is the set of values of y for which there can be a value of g(y).
Here g(y) can be real only if y is greater than or equal to 0.
∴ The domain of the given function is [0,∞) .
10. Given : y is a function of x.
Definition of function : A function is a relation that associates each element in the domain to one element of another set, the co-domain of the function.
∴ For each element x, in the domain, there is only one value of y in the range.