An office uses paper drinking cups in the shape of a cone, with dimensions as shown. To the nearest tenth of a cubic inch, what is the volume of each drinking cup?

Question

asked Jul 1, 2019 72.6k views

2 Answers

Tadamhicks · Answer 1 · 2019-07-03T14:54:24+0000

ANSWER

$Volume\approx 7.90 in^3$

to the nearest tenth

Step-by-step explanation

The given cup has the shape of a cone with dimension,

height=4in.

and

diameter=2(3)/(4)in.

The formula for calculating the area of a cone is given by;

$Volume=(1)/(3) \pi r^2h.$

Where r is the radius of the circular base.

We therefore divide the diameter in to two to find the radius.

This implies that,

r=2(3)/(4) /2

r=(11)/(4) /2

r=(11)/(4) * (1)/(2)

r=(11)/(8)

We now plug in all the above in to the formula, to get,

$Volume=(1)/(3) \pi ((11)/(8))^2*4$

$Volume=(121)/(48) \pi$

Volume=7.918

$Volume\approx 7.90 in^3$

to the nearest tenth

Mohsen Nazari · Answer 2 · 2019-07-05T20:04:45+0000

The volume of a cone is given by the formula
$V=(1)/(3) \pi r^(2) h$

If we plug in the known information into the formula, we will get the answer.

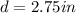
d=2.75 in

We know radius is half of d, so
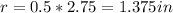
r=0.5*2.75=1.375 in

The height is given as 4 in.

Pluggin all of these in the original formula gives us:

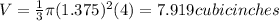
$V=(1)/(3) \pi (1.375)^(2) (4)=7.919 cubic inches$

Rounded to the nearest tenth, our final answer is:

V=7.9 cubic inches