Which compound inequality could this graph be the solution of?

Question

asked Mar 22, 2019 126k views

2 Answers

Tamouse · Answer 1 · 2019-03-26T15:22:01+0000

Answer:

B. 2x + 3 ≥ 11 or 4x - 7 ≤ 1

Explanation:

Given compound inequality,

In option A,

2x + 3 ≥ 11 and 4x - 7 ≤ 1

⇒ 2x ≥ 8 and 4x ≤ 8

⇒ x ≥ 4 and x ≤ 2

$\implies [4,\infty)\cap (-\infty, 2]$

$=\phi$

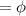
2x + 3 ≥ 11 and 4x - 7 ≤ 1 can not be the correct inequality,

In option B,

2x + 3 ≥ 11 or 4x - 7 ≤ 1

⇒ 2x ≥ 8 or 4x ≤ 8

⇒ x ≥ 4 or x ≤ 2

$\implies [4,\infty)\cup (-\infty, 2]$

Which is shown in the given graph,

Thus, 2x + 3 ≥ 11 or 4x - 7 ≤ 1 is the correct compound inequality,

In option C,

2x + 3 > 11 or 4x - 7 < 1

⇒ 2x > 8 or 4x < 8

⇒ x > 4 or x < 2

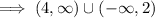
$\implies (4,\infty)\cup (-\infty, 2)$

So, which is not shown in the graph,

2x + 3 > 11 or 4x - 7 < 1 can not be the correct compound inequality,

In option D,

2x + 3 ≥ 11 or 4x - 7 ≥ 1

⇒ 2x ≥ 8 or 4x ≥ 8

⇒ x ≥ 4 or x ≥ 2

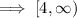
$\implies [4,\infty)$

Which is not shown in the graph,

2x + 3 ≥ 11 or 4x - 7 ≥ 1 is not the correct compound inequality.