Answer:
B. 2x + 3 ≥ 11 or 4x - 7 ≤ 1
Explanation:
Given compound inequality,
In option A,
2x + 3 ≥ 11 and 4x - 7 ≤ 1
⇒ 2x ≥ 8 and 4x ≤ 8
⇒ x ≥ 4 and x ≤ 2
![\implies [4,\infty)\cap (-\infty, 2]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/molwdlo0vpyvgpo0qfuq2alb9725zijtn6.png)
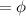
2x + 3 ≥ 11 and 4x - 7 ≤ 1 can not be the correct inequality,
In option B,
2x + 3 ≥ 11 or 4x - 7 ≤ 1
⇒ 2x ≥ 8 or 4x ≤ 8
⇒ x ≥ 4 or x ≤ 2
![\implies [4,\infty)\cup (-\infty, 2]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/97lzfly70orijuin6930xp8xfmgdl154ds.png)
Which is shown in the given graph,
Thus, 2x + 3 ≥ 11 or 4x - 7 ≤ 1 is the correct compound inequality,
In option C,
2x + 3 > 11 or 4x - 7 < 1
⇒ 2x > 8 or 4x < 8
⇒ x > 4 or x < 2
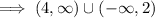
So, which is not shown in the graph,
2x + 3 > 11 or 4x - 7 < 1 can not be the correct compound inequality,
In option D,
2x + 3 ≥ 11 or 4x - 7 ≥ 1
⇒ 2x ≥ 8 or 4x ≥ 8
⇒ x ≥ 4 or x ≥ 2
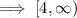
Which is not shown in the graph,
2x + 3 ≥ 11 or 4x - 7 ≥ 1 is not the correct compound inequality.