Question

If the relative errors of three quantities to be multiplied together are 0.009, 0.006 and 0.003, what is the relative error of the resulting quantity? Give your answer to three decimal places

Answer 1

Answer: The relative error of the resulting quantity is 0.018.

Explanation: Relative error of the quantities when are multiplied together is usually less than or equal to the sum of each relative error. Mathematically, it is represented as

`\delta x=(\Delta x)/(x)`

According to the question,

Let us assume that the three quantities are
`r_1,r_2\text{ and }r_3`

`r=r_1* r_2* r_3`

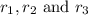
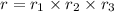
Taking log on both the sides, we get

`log(r)=log(r_1* r_2* r_3)`

`log(r)=log(r_1)+log(r_2)+log(r_3)`

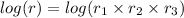
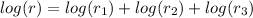
Relative error is calculated by:

`(\delta r)/(r)=(\delta r_1)/(r_1)+(\delta r_2)/(r_2)+(\delta r_3)/(r_3)`

`(\delta r)/(r)=0.009+0.006+0.003=0.018`

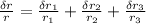
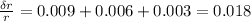
This value has 3 significant figures only, so the resulting relative error is 0.018.