Question

Can someone help me on 14&15

Answer 1

For 14, I think the definition of the absolute value will make things easier. Recall that

`|x|=\begin{cases}x&\text{for }x\ge0\\-x&\text{for }x<0\end{cases}`

So we have

`|x-3|=\begin{cases}x-3&\text{for }x\ge3\\3-x&\text{for }x<3\end{cases}`

`|x+1|=\begin{cases}x+1&\text{for }x\ge-1\\-x-1&\text{for }x<-1\end{cases}`

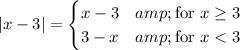
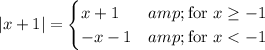
Putting these together, we have 3 different cases to consider:

`f(x)=\begin{cases}(3-x)-2(-x-1)=x+5&\text{for }x<-1\\(3-x)-2(x+1)=1-3x&\text{for }-1\le x<3\\(x-3)-2(x+1)=-x-5&\text{for }x\ge3\end{cases}`

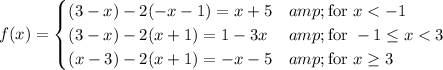
Then we check the derivative, noting that we shouldn't expect the derivative to be continuous at
`x=-1` and
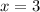`x=3`, so we ignore those exact cases:

`f'(x)=\begin{cases}1&\text{for }x<-1\\-3&\text{for }-1<x<3\\-1&\text{for }x>3\end{cases}`

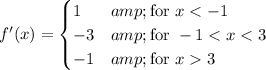
This tells us that
`f(x)` is increasing on
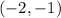`(-2,-1)` and decreasing on
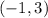`(-1,3)`. We know that
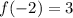`f(-2)=3` and
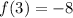`f(3)=-8`, but if we can verify that
`f(x)` is continuous at
`x=-1`, then we can use the trends from the derivative test above to show there's at least a local maximum at that point.

We have
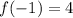`f(-1)=4`, while

`\displaystyle\lim_(x\to-1^-)f(x)=\lim_(x\to-1)x+5=4`

`\displaystyle\lim_(x\to-1^+)f(x)=\lim_(x\to-1)1-3x=4`

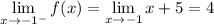
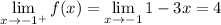
so
`f(x)` is indeed continuous. So,
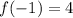`f(-1)=4` is an absolute maximum and
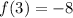`f(3)=-8` is an absolute minimum.

For 15, the fact that
`f` is differentiable and attains an extreme value at
`x=2` means that
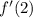`f'(2)` exists, and that
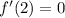`f'(2)=0`. Then for part (a),

`g(2)=2f(2)+1=1`

`h(2)=2f(2)+2+1=3`

`g'(2)=f(2)+2f'(2)=0`

`h'(2)=f(2)+2f'(2)+1=1`

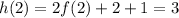
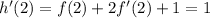
For part (b), in order for
`g` or
`h` to have extreme values at
`x=2`, we would need to have
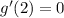`g'(2)=0` (which is true, as shown above) and
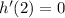`h'(2)=0` (which is not).