The antibiotic clarithromycin is eliminated from the body according to the formula
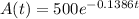
where A is the amount remaining in the body (in milligrams) t hours after the drug reaches peak concentration
We need to find the time 't' when amount of drug is reduced to 100
Plug in 100 for A(t) and solve for t
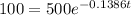
Divide both sides by 500
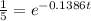
Take ln on both sides
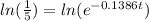
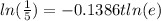
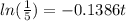
divide both sides by -0.1386
t = 11.6121
11.61 hours will pass before the amount of drug in the body is reduced to 100.