Answer: The area of ABC is 56 m².
Step-by-step explanation:
It is given that in △ABC, point P∈ AB is so that AP:BP=1:3 and point M is the midpoint of segment CP.
Since point P divides the line AB in 1:3, therefore the area of triangle APC and BPC is also in ratio 1:3. To prove this draw a perpendicular h on AB from C.
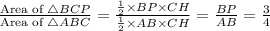
Since the area of BPC is
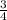 th part of total area, therefore area of APC is
th part of total area, therefore area of APC is
 th part of total area.
th part of total area.
The point M is the midpoint of CP, therefore the area of BMP and BMC is equal by midpoint theorem.
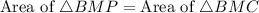
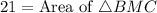
Area of BPC is,
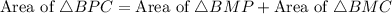
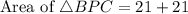
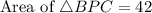
Area of APC is,

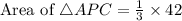
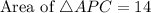
Area of ABC is,
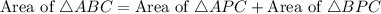

Therefore, the area of ABC is 56 m².