Question

n △ABC, point P∈ AB is so that AP:BP=1:3 and point M is the midpoint of segment CP. Find the area of △ABC if the area of △BMP is equal to 21m^2.

Answer 1

Answer: The area of ABC is 56 m².

Step-by-step explanation:

It is given that in △ABC, point P∈ AB is so that AP:BP=1:3 and point M is the midpoint of segment CP.

Since point P divides the line AB in 1:3, therefore the area of triangle APC and BPC is also in ratio 1:3. To prove this draw a perpendicular h on AB from C.

`\frac{\text{Area of } \triangle BCP}{\text{Area of } \triangle ABC} =((1)/(2)* BP* CH)/((1)/(2)* AB* CH) =(BP)/(AB)= (3)/(4)`

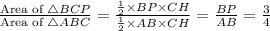
Since the area of BPC is
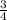`(3)/(4)`th part of total area, therefore area of APC is
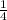`(1)/(4)`th part of total area.

The point M is the midpoint of CP, therefore the area of BMP and BMC is equal by midpoint theorem.

`\text{Area of } \triangle BMP=\text{Area of } \triangle BMC`

`21=\text{Area of } \triangle BMC`

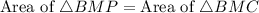
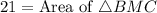
Area of BPC is,

`\text{Area of } \triangle BPC=\text{Area of } \triangle BMP+\text{Area of } \triangle BMC`

`\text{Area of } \triangle BPC=21+21`

`\text{Area of } \triangle BPC=42`

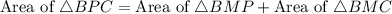
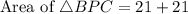
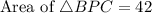
Area of APC is,

`\text{Area of } \triangle APC=(1)/(3)* \text{Area of } \triangle BPC`

`\text{Area of } \triangle APC=(1)/(3)* 42`

`\text{Area of } \triangle APC=14`

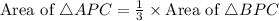
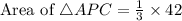
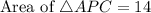
Area of ABC is,

`\text{Area of } \triangle ABC=\text{Area of } \triangle APC+\text{Area of } \triangle BPC`

`\text{Area of } \triangle ABC=14+42=56`

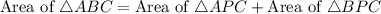
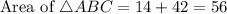
Therefore, the area of ABC is 56 m².