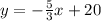Question

What is the y-intercept of the equation of the line that is perpendicular to the line y =3/5x + 10 and passes through the point (15, –5)? The equation of the line in slope-intercept form is y = -5/3x + .

Answer 1

The answe would be y=-5/3x+20

Answer 2

Equation of the line in the slope-intercept form will be
`y=-(5)/(3)x+20`

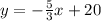
Explanation:

An equation of the line perpendicular to
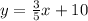`y=(3)/(5)x+10` will be in the form of y = mx + c

Where m = slope of the line

c = y intercept of the line

From the property of the perpendicular line

`m_(1)* m_(2)=-1`

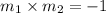
where
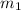`m_(1)` and
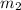`m_(2)` are the slopes of the perpendicular lines.

If
`m_(1)` =
`(3)/(5)`

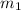then
`(3)/(5)* m_(2)=-1`

`m_(2)=-(5)/(3)`

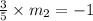
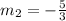
So the equation will be
`y=-(5)/(3)x+c`

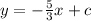
This line passes through the point (15, -5)

`(-5)=-(5)/(3)(15)+c`

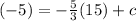
-5 = -25 + c

c = 25 - 5

c = 20

Finally the equation will be
`y=-(5)/(3)x+20`