Answer:
Equation of the line in the slope-intercept form will be

Explanation:
An equation of the line perpendicular to
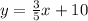 will be in the form of y = mx + c
will be in the form of y = mx + c
Where m = slope of the line
c = y intercept of the line
From the property of the perpendicular line

where
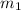 and
and
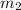 are the slopes of the perpendicular lines.
are the slopes of the perpendicular lines.
If
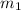 =
=

then
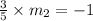
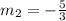
So the equation will be
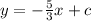
This line passes through the point (15, -5)
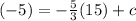
-5 = -25 + c
c = 25 - 5
c = 20
Finally the equation will be
