Answer:

Explanation:
The area of
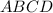 is comprised of two triangles, so we can find the area of both triangles and add them to get the total area of
is comprised of two triangles, so we can find the area of both triangles and add them to get the total area of
Since the sum of the interior angles of a triangle add up to
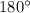 , we have:
, we have:
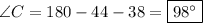 .
.
The Law of Sines is given as:
 for any triangle.
for any triangle.
Therefore, we have the proportion:
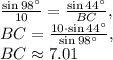 .
.
Now that we have two sides of a triangle and the angle between them, we can use
![[\triangle]=(1)/(2)ab\sin C](https://img.qammunity.org/2022/formulas/mathematics/high-school/culo6zbje7e53nqc3ipxbn9fa23nbmkekj.png) to find the area of
to find the area of
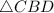 :
:
![[CBD]=(1)/(2)\cdot 10\cdot 7.01 \cdot \sin 38^(\circ),\\\\\left [CBD]\right\approx 21.58](https://img.qammunity.org/2022/formulas/mathematics/high-school/ahxx2qhhko1bhtfo8nd4z5abi7t71zp370.png) .
.
Since
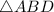 is a right triangle, we can use basic trig rules for a right triangle to solve for the sides:
is a right triangle, we can use basic trig rules for a right triangle to solve for the sides:
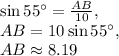 ,
,
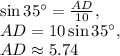 .
.
Therefore, the area of
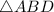 is:
is:
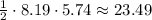 .
.
The area of
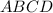 is then
is then
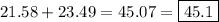 .
.
 Note that intermediate results were rounded during this calculation. Therefore, there is a small margin of error when rounding to final answer to one decimal place. I recommend plugging in values for yourself using all equations I wrote above, then rounding only your final answer to one decimal place as requested by the problem.
Note that intermediate results were rounded during this calculation. Therefore, there is a small margin of error when rounding to final answer to one decimal place. I recommend plugging in values for yourself using all equations I wrote above, then rounding only your final answer to one decimal place as requested by the problem.