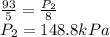Answer: New pressure inside the flask would be 148.8 kPa.
Explanation: The combined gas law equation is given by:
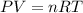
As the flask is a closed flask, so the volume remains constant. Temperature is constant also.
So, the relation between pressure and number of moles becomes
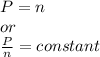
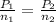
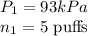
- Final conditions: When additional 3 puffs of air is added
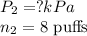
Putting the values, in above equation, we get