the graph of 13y + kx = 4 and the line containing the points (5, -8) and (2, 4) are parallel.
We find the slope of parallel line using two given points
(5, -8) and (2, 4)
Slope formula is
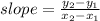
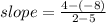

so slope = -4
Slope of any two parallel lines are always equal
Lets find the slope of the equation 13y + kx = 4
Subtract kx on both sides
13 y = -kx + 4
Divide both sides by 13
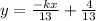
Now slope = -k/13
We know slope of parallel lines are same
So the slope of 13y + kx = 4 is also -4
Hence we equation the slope and find out k
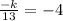
Multiply by 13 on both sides and divide by -1
k = 52
the value of k = 52