Question

Find the value of k so that the graph of 13y + kx = 4 and the line containing the points (5, -8) and (2, 4) are parallel.

Answer 1

ooh, so paralell lines have the same slope

find the slope of the line passing thorugh those 2 points

slope=rise/run=(y1-y2)/(x1-x2)

for (5,-8) and (2,4)

slope=(-8-4)/(5-2)=-12/3=-4

so find k such that the slope of the other equation is -4

for ax+by=c, the slope is -a/b

for 13y+kx=4, the slope is -k/13

-k/13=-4

multiply both sides by 13

-k=-52

divide both sides by -1

k=52

Answer 2

the graph of 13y + kx = 4 and the line containing the points (5, -8) and (2, 4) are parallel.

We find the slope of parallel line using two given points

(5, -8) and (2, 4)

Slope formula is

`slope = (y_2-y_1)/(x_2-x_1)`

`slope = (4-(-8))/(2-5)`

`slope = (12))/(-3)=-4`

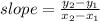
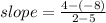
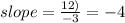
so slope = -4

Slope of any two parallel lines are always equal

Lets find the slope of the equation 13y + kx = 4

Subtract kx on both sides

13 y = -kx + 4

Divide both sides by 13

`y= (-kx)/(13) + (4)/(13)`

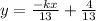
Now slope = -k/13

We know slope of parallel lines are same

So the slope of 13y + kx = 4 is also -4

Hence we equation the slope and find out k

`(-k)/(13)=-4`

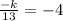
Multiply by 13 on both sides and divide by -1

k = 52

the value of k = 52