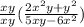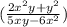Question

SIMPLIFY THE EXPRESSION... PLEASE HELP :(

Answer 1

remember
`((a)/(b))/((c)/(d))=((a)/(b))((d)/(c))=(ad)/(bc)`

try to combine fractions in numerator and denomenator

numerator:
`(1)/(x)+(2)/(y)`

make common denom

multiply left one by
`(y)/(y)` and right one by
`(x^2)/(x^2)`

`(y)/(yx^2)+(2x^2)/(yx^2)=(2x^2+y)/(yx^2)`

denomenator

`(5)/(x)-(6)/(y^2)`

make common denom

multiply left one by
`(y^2)/(y^2)` and right one by
`(x)/(x)`

`(5y^2)/(xy^2)-(6x)/(xy^2)=(5y^2-6x)/(xy^2)`

combining we get

`((1)/(x^2)+(2)/(y))/((5)/(x)-(6)/(y^2))=`

`((2x^2+y)/(yx^2))/((-6x+5y^2)/(xy^2))=`

`((2x^2+y)/(yx^2))((xy^2)/(-6x+5y^2))=`

`(2x^3y^2+xy^3)/(-6x^3y+5x^2y^3)=`

`((2x^2y+y^2)/(-6x^2+5xy))((xy)/(xy))=`

`((2x^2y+y^2)/(-6x^2+5xy))(1)=`

`(2x^2y+y^2)/(-6x^2+5xy)`

Answer 2

The simplified version of the given expression is
`((2x^2y+y^2)/(5xy-6x^2) )`

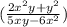
Explanation:

We are given an expression which is a complex fraction:

`((1)/(x^2) +(2)/(y) )/((5)/(x) +(6)/(y^2) )`

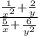
We can take LCM of these fractions to get:

`((y+2x^2)/(x^2y) )/((5y^2-6x)/(xy^2) )`

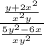
Taking the reciprocal of the lower fraction to change it to multiplication:

`(y+2x^2)/(x^2y)` ×
`(xy^2)/(5y^2-6x)`

`(2x^2y+xy^3)/(5x^2y^3-6x^3y)`

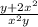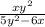
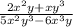
Taking xy as common from both the numerator and the denominator to get:

`(xy)/(xy) ((2x^2y+y^2)/(5xy-6x^2) )`

`((2x^2y+y^2)/(5xy-6x^2) )`