Question

A pendulum is set swinging. its first oscillation is through 30 and each succeeding oscillation is through 95% of the angle of the one before it. After how many swings is the angle through which it swings less than 1 degree?

Answer 1

After 76 swings the angle through which it swings less than 1°

Solution-

From the question,

Angle of the first of swing = 30° and then each succeeding oscillation is through 95% of the angle of the one before it.

So the angle of the second swing =
`(30* (95)/(100))^(\circ)`

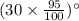
Then the angle of third swing =
`(30* ((95)/(100))^2)^(\circ)`

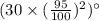
So, this follows a Geometric Progression.

`(30,\ 30\cdot (95)/(100),\ 30\cdot ((95)/(100))^2............,0)`

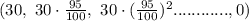
a = The initial term = 30

r = Common ratio =
`(95)/(100)`

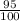
As we have to find the number swings when the angle swept by the pendulum is less than 1°.

So we have the nth number is the series as 1, applying the formula

`T_n=ar^(n-1)`

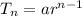
Putting the values,

`\Rightarrow 1=30((95)/(100))^(n-1)`

`\Rightarrow (1)/(30) =((95)/(100))^(n-1)`

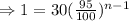
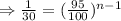
Taking logarithm of both sides,

`\Rightarrow \log (1)/(30) =\log ((95)/(100))^(n-1)`

`\Rightarrow \log (1)/(30) =(n-1)\log ((95)/(100))`

`\Rightarrow -1.5=(n-1)(-0.02)`

`\Rightarrow 1.5=(n-1)(0.02)`

`\Rightarrow n-1=(1.5)/(0.02)`

`\Rightarrow n-1=75`

`\Rightarrow n=76`

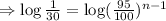
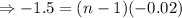
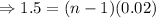
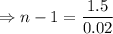
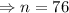
Therefore, after 76 swings the angle through which it swings less than 1°