Answer-
After 76 swings the angle through which it swings less than 1°
Solution-
From the question,
Angle of the first of swing = 30° and then each succeeding oscillation is through 95% of the angle of the one before it.
So the angle of the second swing =
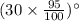
Then the angle of third swing =
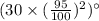
So, this follows a Geometric Progression.
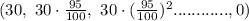
a = The initial term = 30
r = Common ratio =
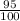
As we have to find the number swings when the angle swept by the pendulum is less than 1°.
So we have the nth number is the series as 1, applying the formula
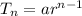
Putting the values,
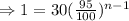
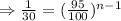
Taking logarithm of both sides,
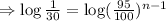
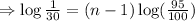
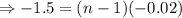
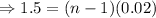
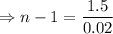
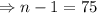
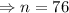
Therefore, after 76 swings the angle through which it swings less than 1°