Question

How many complex zeros does the polynomial function have?
f(x)=−3x^6−2x^4+5x+6

Answer 1

The given polynomial function has 6 complex zeros.

Step-by-step explanation:

The given polynomial function is f(x) = -3x⁶ - 2x⁴ + 5x + 6.

To determine the number of complex zeros, we need to use the Fundamental Theorem of Algebra, which states that for a polynomial of degree n, there are exactly n complex zeros (including repeats or multiplicities).

In this case, the highest degree of the polynomial is 6, so there are exactly 6 complex zeros.

Answer 2

one way would be to factor

I can't factor it so we will have to use Descartes' Rule of Signs which is helpful for finding how many real roots you have

it goes like this:

for a polynomial with real coefients, consider
`f(x)=-3x^6-2x^4+5x+6`.

after arranging the terms in decending order in terms of degree, count how many times the signs of the coeffients change direction and minus 2 from that number until you get to 1 or 0. that will be the number of even roots the function can have

We have (-, -, +, +). the signs changed 1 times, so it has 1 real positive root

to get the negative roots, we evaluate f(-x) and see how many times the root changes

`f(-x)=-3x^6-2x^4-5x+6`

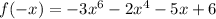
signs are (-, -, -, +). there was 1 change in sign

so the function has 1 real negative root

a total of 2 real roots

a function of degree
`n` can have at most,
`n` roots

our function is degree 6 so it has 6 roots

if 2 are real, then the others must be complex

6-2=4 so there are 4 complex roots

you can also show that there are only 2 real roots by using a graphing utility to see that there are only 2 real roots