Answer:
20 mL
Explanation:
Let x represent the amount of 20% solution added and y represent the amount of 60% solution added.
Our first equation would be
x + y = 80,
since the amount of 20% solution and the amount of 60% solution combine to make a total of 80 milliliters.
20% = 20/100 = 0.2; this means the 20% solution would be represented as 0.2x.
60% = 60/100 = 0.6; this means the 60% solution would be represented as 0.6y.
Together they make 80 milliliters of a 50% solution; this gives us the equation
0.2x + 0.6y = 0.8(50)
Simplifying,
0.2x + 0.6y = 40
This gives us the system
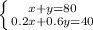
To solve this, we will use elimination. Multiply the top equation by 0.2 to make the coefficients of x the same:
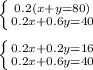
Subtract the bottom equation from the first:
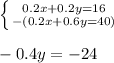
Divide both sides by -0.4:
-0.4y/-0.4 = -24/-0.4
y = 60
There should be 60 milliliters of 60% solution.
Substitute this into the first equation:
x+60 = 80
Subtract 60 from each side:
x+60-60 = 80-60
x = 20
There should be 20 milliliters of the 20% solution.