Question

Can someone explain how to do 60 and 62?

Answer 1

In question 60, the base change property was used.

This property says that:

`log_b(c) = (log_d(c))/(log_d(b))`

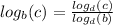
Remember that the base of the neperian logarithm (ln) is the number of euler "e"
`ln(a) = log_e(a)`

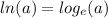
So:

`log_9(64) = (ln(64))/(ln(9))`

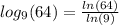
Option C

In question 62, use the base change property again. We have:

`log_(1/2)(x ^ 2)`

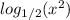
Let's change the
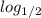`log_(1/2)` to the
`log_2.`

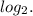
So:

`log_(1/2)(x ^ 2) = (log_2(x ^ 2))/(log_2 (1/2))` ----------- lower the exponent in the numerator
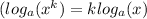`(log_a(x ^ k) = klog_a( x)`) and calculate the log of the denominator.

`= (2log_2(|x|))/(- 1)`

`log_(1/2)(x ^ 2) = -2log_2(|x|)`

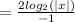
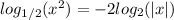
Answer:

Option E