Question

For what value of x is PQ BC pls look at picture

Answer 1

Let us assume PQ || BC.
Then, by Basic Proportionality Theorem, we get,
AP/PB = AQ/QC
=> x/(x+7) = (x-3)/(x+1)
=> x (x+1) = (x+7)(x-3)
=> x^2 + x = x^2 - 3x + 7x - 21
=> x = 4x - 21
=> -4x + x = -21
=> -3x = -21
=> 3x = 21
=> x = 21/3
=> x = 7
Therefore, for PQ||BC the value of x should be 7

Answer 2

x = 7

Explanation:

According to the proportionality theorem of triangles, if a line parallel to one side of a triangle intersects the rest of the two sides, then the line divides these two sides proportionally.

So,
`(AP)/(PB) = (AQ)/(QC)`

Putting in the values to get:

`(x)/(x+7) = (x-3)/(x+1)`

`x(x+1) = (x-3)(x+1)`

`x^2+x=x^2+7x-3x-21`

`7x-3x-x= 21`

`3x=21`

`x=7`

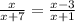
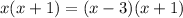
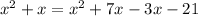
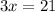
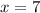
Therefore, the value of
`x` in this case is equal to 7.