Answer:
x = 7
Explanation:
According to the proportionality theorem of triangles, if a line parallel to one side of a triangle intersects the rest of the two sides, then the line divides these two sides proportionally.
So,
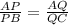
Putting in the values to get:
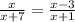
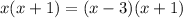
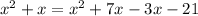

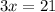
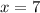
Therefore, the value of
 in this case is equal to 7.
in this case is equal to 7.