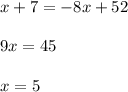Question

Help
Solve the following exponential equation for x. Show your work step by step.

Answer 1

Given:

The equation

`5^(x+7)=((1)/(625))^(2x-13)`

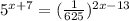
Answer:

`x=5`

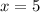
Explanation:

To simplify the given expression, we use the Laws of Exponents; that is, when the bases are the same in two sides of the equation, the exponents can be equated.

So, we begin by expressing 625 on the right hand side as a power of 5 which is the same base as on the left hand side.

Then, we equate the exponents and simplify for x as we usually do.

The following is the solution.

We know

`625=5^(4)\\\\</p><p>`

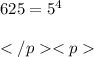
and

`(1)/(625)=5^(-4)\\\\`

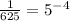
So,

`5^(x+7)=((1)/(625))^(2x-13)\\\\5^(x+7)=((1)/(625))^(2x-13)=(5^(-4))^(2x-13)=5^(-8x+52)\\\\`

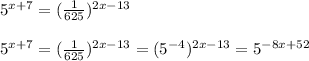
We now equate the exponents on both sides as solve for x like we would normally do

`x+7=-8x+52\\\\9x=45\\\\x=5`