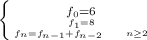Question

Write an recrusive equation of 6,8,14,22,36,58

Answer 1

This is A Fibonacci Sequence where the next term is the SUM of the two previous terms:

an = a1 + f × (n-1)

Answer 2

The recursive equation for the given sequence is:

`\left \{ {{f_(0) = 6} \atop {{f_(1) = 8} \atop {f_(n) = f_(n-1) + f_(n-2)\hspace{0.5cm}n \geq 2}}} \right.`

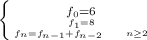
Explanation:

Starting with 6 and 8, the next term is the sum of the two previous terms. This is a Fibonacci Sequence with initial values 6 and 8.

We can write the initial values as:

`f_(0) = 6 \\ f_(1) = 8`

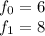
Since the next term of the sequence is the sum of the two previous ones, the recursive step can be stated as follows:

`f_(n) = f_(n-1) + f_(n-2) \hspace{0.8cm}n \geq 2`

Notice that this step needs the initial values and can only be calculate for values of n equal or greater than 2.

Finally the recursive equation is:

`\left \{ {{f_(0) = 6} \atop {{f_(1) = 8} \atop {f_(n) = f_(n-1) + f_(n-2)\hspace{0.5cm}n \geq 2}}} \right.`