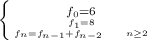Answer:
The recursive equation for the given sequence is:
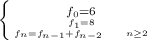
Explanation:
Starting with 6 and 8, the next term is the sum of the two previous terms. This is a Fibonacci Sequence with initial values 6 and 8.
We can write the initial values as:
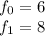
Since the next term of the sequence is the sum of the two previous ones, the recursive step can be stated as follows:
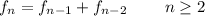
Notice that this step needs the initial values and can only be calculate for values of n equal or greater than 2.
Finally the recursive equation is: